Publications
Non-Asymptotic Error Bounds for SMC with Biased Proposals: Application to Conditional Diffusion Sampling
Sequential Monte Carlo (SMC) methods are a natural tool for post-hoc conditioning of pretrained generative models, but in many applications the mutation kernels used by the particle system are biased approximations of an ideal Feynman--Kac flow. This paper develops a non-asymptotic error analysis for such SMC samplers. Under forward-smoothing forgetting conditions, we decompose the total error into a kernel bias, measuring the effect of replacing the ideal transition kernels by approximate ones, and a finite-particle Monte Carlo error. Our approach relies on extending local Doeblin-type conditions and Lyapunov drift arguments for Markov kernels to conditional distributions, thereby enabling a principled control of the bias. We then instantiate this general framework for conditional sampling with score-based diffusion models, and derive the first non-asymptotic error bound that jointly controls initialization error, time discretization, and score approximation in the reverse diffusion dynamics as well as finite-particle Monte Carlo error.
On Forgetting and Stability of Score-based Generative Models
Understanding the stability and long-time behavior of generative models is a fundamental problem in modern machine learning. This paper provides quantitative bounds on the sampling error of score-based generative models by leveraging stability and forgetting properties of the Markov chain associated with the reverse-time dynamics. Under weak assumptions, we identify two structural conditions ensuring propagation control of initialization and discretization errors of the backward process: a Lyapunov drift condition and a Doeblin-type minorization condition. A practical consequence is quantitative stability of the sampling procedure, as the reverse diffusion dynamics induces a contraction mechanism along the sampling trajectory. Overall, the results clarify the role of stochastic dynamics in score-based models and provide a principled framework to analyze error propagation in such approaches.
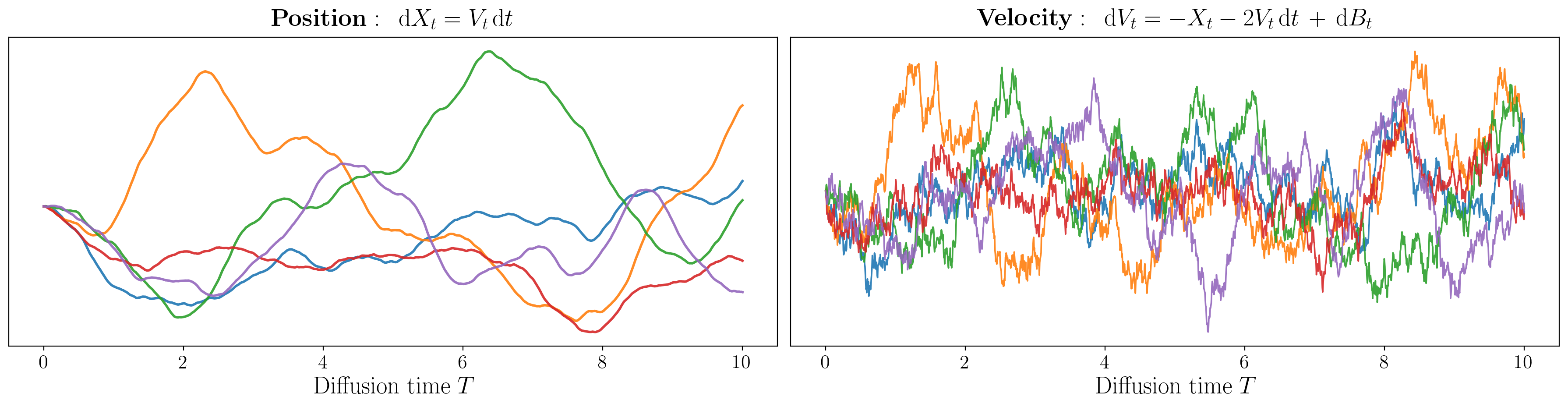
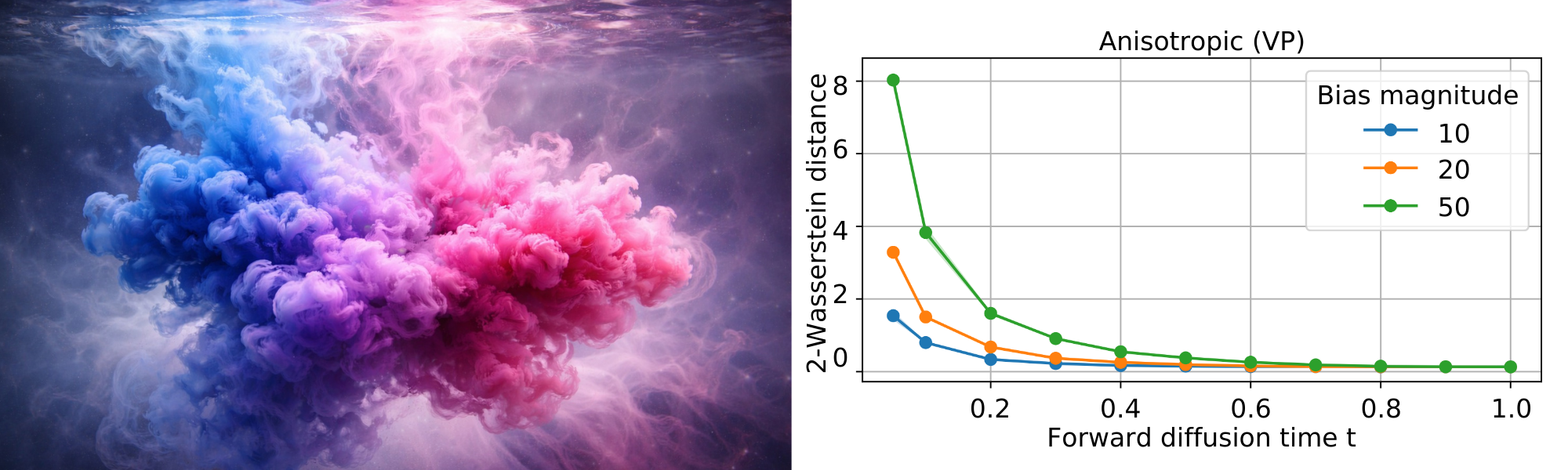
Wasserstein Convergence of Critically Damped Langevin Diffusions
We study the convergence guarantees of Critically Damped Langevin Diffusions (CLDs) for score-based generative modeling and provide, to the best of our knowledge, the first Wasserstein-2 upper bound for kinetic SGMs by analyzing the Lipschitz regularity of a modified score function. Our study also motivates the introduction of a noise–control hyperparameter that restores ellipticity by injecting noise across the entire state space. This choice has a measurable impact on generation quality in synthetic datasets.
An Analysis of the Noise Schedule for Score-based Generative Models
We study how the choice of the noise schedule impacts the generation error in Score-based Generative Models (SGMs). We derive explicit upper bounds for both the Kullback–Leibler divergence and the Wasserstein-2 distance between the generated and target distributions, highlighting their dependence on model hyperparameters and regularity of the data distribution. Theoretical findings are supported by numerical experiments on synthetic and real datasets.
You can also find my articles on my Google Scholar profile.